【数Ⅰ】勘に頼らずにできる！因数分解のツボ（３）

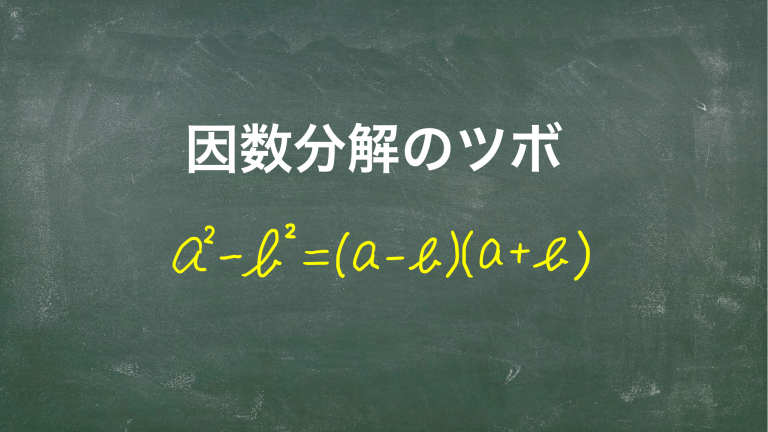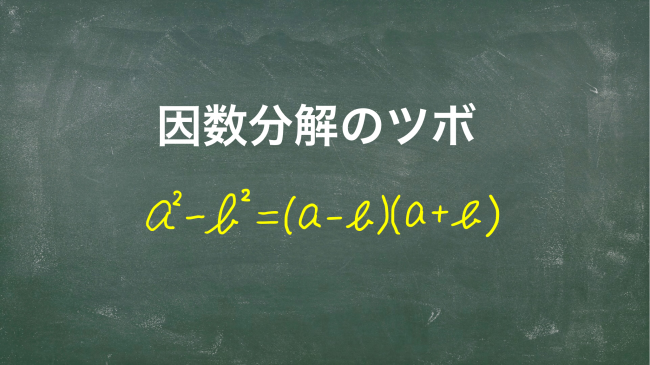
前回に続き，因数分解のツボについての記事です。

勘に頼っていると，解けるときと解けないときがあるはずです。

必ず解けるようになるために，正しい手順を身につけましょう。

前回と前々回の記事はこちらです。

勘に頼らずにできる！因数分解のツボ（１）

勘に頼らずにできる！因数分解のツボ（２）

覚えておきたいテクニック
複雑なものをシンプルに見せる”置き換え”
初めて見たときは「反則だ！」と叫びたくなる”複2次式”
覚えておきたい公式
この記事のまとめ

覚えておきたいテクニック

因数分解をするうえで，最も大切なことは前回の記事で伝えた「次数の低い文字について整理する」ことです。

そうでした。ちゃんと覚えてるっス。

ただ，できればもう少し知っておきたいことがある。知らないと，解けるけれども大変な苦労をしなければならないことがあるからね。

「苦労は買ってでもしろ」ということわざもありますけどね。

数学においても苦労した方がいい場面はある。でも，いつもいつも苦労する計算をするのは非効率的だ。ちょっと工夫することで計算の手間が省けたりするので，積極的に習得してほしい。

了解っス。

では紹介しよう。入試において習得すべき手法は次の3つだ。

複雑なものをシンプルに見せる”置き換え”

まず最初のテクニックは「置き換え」です。典型的な問題として，次の例題を見てみましょう。

次の式を因数分解しなさい。

\(x^4+x^2-2\)
\(x(x+1)(x+2)(x+3)-24\)

どこから手を付けるかな・・・あ，置き換えだから，\(x^2~\)を\(~t~\)と置き換えたりするのかな？

冴えてるねえ。(1)はそれでいけます。(2)はちょっと難しいよ。いきなり置き換えるのではなく，一部だけ展開したあとに置き換えます。一度は経験しておかないと難しいかな。

何か悔しいなあ。絶対解いてやる。ええと・・・・。

(1) \(\quad \)途中で\(~x^2=t~\)と置き換える。 \begin{align*} x^4+x^2-2&=t^2+t-2 \\ &=(t-1)(t+2) \\ &=(x^2-1)(x^2+2) \\ &=(x-1)(x+1)(x^2+2) \end{align*} (2) \(\quad \)途中で\(~x^2+3x=A~\)と置き換える。 \begin{align*} x(x+1)(x+2)(x+3)-24&=x(x+3) \times (x+1)(x+2) -24 \\ &=(x^2+3x)(x^2+3x+2)-24 \\ &=A(A+2)-24 \\ &=A^2+2A-24 \\ &=(A-4)(A+6) \\ &=(x^2+3x-4)(x^2+3x+6) \\ &=(x-1)(x+4)(x^2+3x+6) \end{align*}

ふう。なんとかできたけど，難しいっスね。

まあね。(1)は初見で思いつくことができても，(2)は難しいかもね。でも一度経験すれば「ああ，あれかな」と気づくことができるようになるよ。何事も経験が大切なのさ。

初めて見たときは「反則だ！」と叫びたくなる”複2次式”

例題を見てみましょう。

次の式を因数分解せよ。

\(x^4+x^2+1\)
\(x^4+4\)

あれ？(1)はさっきの問題と似てるっスよ。また\(~x^2=t~\)と置き換えて・・・ん？解けない・・・まあいいや。気にせず次の(2)を考えよう・・・？(2)なんて何をどうすればいいのか，きっかけすらわかんないっス！

これらはちょっと特殊な解法と言っていいだろう。実際，教科書によっては載っていないこともある。でも，入試ではたまに見る形なので，ここで一緒に学んでおきましょう。解答は以下の通り。ポイントは，\(a^2-b^2=(a-b)(a+b)\)を利用するために，項を足したり引いたりして調整するところかな。

(1) \begin{align*} x^4+x^2+1&=(x^4+2x^2+1)-x^2 \\ &=(x^2+1)^2-x^2 \\ &=\left\{ (x^2+1)-x \right\} \left\{ (x^2+1)+x \right\} \\ &=(x^2-x+1)(x^2+x+1) \end{align*} (2) \begin{align*} x^4+4&=(x^4+4x^2+4)-4x^2 \\ &=(x^2+2)^2-(2x)^2 \\ &=\left\{ (x^2+2)-2x \right\} \left\{ (x^2+2)+2x \right\} \\ &=(x^2-2x+2)(x^2+2x+2) \end{align*}

ちょちょ・・・ちょっと待ってくださいよ。何スかこれ。こんなの思いつくわけないっスよ。もともと無かったものを足したり引いたりして，反則じゃないっすか！

ははは！シンジ君がそう言いたくなるのも無理はない。何を隠そう，私も高校生のとき同じことを言ったよ，「こんなの反則だ！」てね。でも，単純にうまいなあ，凄いなあ，と思わないかい？

・・・確かに。自分で思いつくことはできないけど，考えた人はすごいなあって思うっス。

だろう？数学を学んでいると，こんなことはよくあるんだ。そして，最初は反則だ！と思っても，徐々に自分でも使えるようになる。たくさん持っているテクニックの一つになっていくんだ。シンジ君が3つくらい階段を上って力がつくと，こんな問題は数ある簡単な問題に過ぎない，と思えるようになるよ。

・・・だといいっスけどね。

覚えておきたい公式

最後は，覚えておきたい公式です。数Ⅰではなく，数Ⅱの教科書に載っています。教科書によっては載っていないものもあるようです。

覚えておきたい3次式の公式

\(a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\)

入試では普通に使われますので，まとめて覚えておきましょう。例えば次のような問題で使われます。

次の式を因数分解しなさい。

\(x^3+3xy+y^3-1\)
\((x-y)^3+(y-z)^3+(z-x)^3\)

？さっきの公式をどこで使えばいいのか，全然わかんないんスけど。

(1)は，\(-1\)を\( (-1)^3 \)とすればわかるよ。(2)はちょっとうまい置き換えが必要だ。答は以下ね。

(1) \begin{align*} & ~\quad x^3+3xy+y^3-1 \\ &=x^3+y^3+(-1)^3-3\cdot x \cdot y \cdot (-1) \\ &=\left\{ x+y+(-1)\right\} \left\{ x^2+y^2+(-1)^2-xy-y\cdot (-1)-(-1)\cdot x \right\} \\ &=(x+y-1)(x^2-xy+y^2+x+y+1) \end{align*} (2)\(\quad y-z=X,~z-x=Y,~x-y=Z~\)とおく。\(X+Y+Z=0~\)となるので \begin{align*} &\quad (x-y)^3+(y-z)^3+(z-x)^3 \\ &=X^3+Y^3+Z^3 \\ &=(X+Y+Z)(X^2+Y^2+Z^2-XY-YZ-ZX)+3XYZ \\ &=3XYZ \\ &=3(x-y)(y-z)(z-x) \end{align*}

うわー，(2)はまたすげーな。思いつくかな，こんなこと。

ちょっと感動だよね。でも因数分解に限らず，複雑な形を見たら，うまく置き換えてシンプルな形にすることを心がけるといいよ。それにしてもこの問題の解答，美しいよね・・・ってこう思う私は変でしょうか？

変っス。