こんにちは!独学サポートコーチ長宮慶次です。
グラフを描くのが面倒くさいなあ・・・と感じたことはありませんか?
数Ⅱまでなら,3次関数や4次関数だから,概形はすぐに分かります
でも数Ⅲになると,複雑な関数は式を見ただけでは,グラフの概形が分かりませんよね
「だから面倒くさくても,微分して増減表を描かなきゃなあ・・・」
いえいえ,実は,式を見ればグラフの概形は分かるのです。微分しなくても。
その方法をお伝えしましょう
「グラフを描け」という問題では使えません。そのときはちゃんと微分して求めましょう。
微分せずにグラフを描く手順
まずは手順を確認しましょう。そのあと,具体的な関数で練習をしてみます。
手順は以下の通りです。
- 定義域を確認する
- \(~x~\)軸,\(y~\)軸との交点を確認し,グラフが存在する領域を確定する
- 極限を,大まかに調べる
これでOK。大体の形はつかむことができます。
もちろん,極大となるところはどこか,増減の程度はどのくらいか,などの細かいところはわかりません。
でも,そんな細かいところは分からなくても,大体の形が分かればいい場面は多いと思います。
そんなときに役に立ちますので,覚えておきましょう。
練習してみよう
では,具体的な関数で,グラフの形を調べてみましょう。
関数は\(f(x)=\dfrac{e^x}{x-1}\)とします。
定義域を確認する
まずは,式を見て定義域を確認します。
分母は0にならないので,定義域は\(~x \not= 1~\)となります。
分母が0にならない,ルートの中は0以上である,などが定義域に大きく関係します。
この時点で,\(xy\)平面が\(~x < 1 ~\)と\(~x > 1~\)の領域に分けられます。
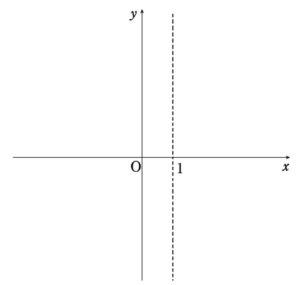
\(~x~\)軸,\(y~\)軸との交点を確認し,グラフが存在する領域を確定する
\(f(x)=\dfrac{e^x}{x-1}\)の分子は\(~e^x~\)なので,\(f(x)\)が\(~0~\)になることはなく,\(x~\)軸との交点は存在しません。
また,\(f(0)=-1~\)なので,\(y~\)軸との交点は\( (0,~-1) \)です。
次に,グラフが存在する領域を考えます。
\(f(x)=e^x \times \dfrac{1}{x-1}\)であり,\(e^x~\)は常に正ですから,\(f(x)~\)の正負は\(\dfrac{1}{x-1}\)の正負で決まります。したがって,\(x>1~\)のとき\(f(x)>0\)であり,\(x<1~\)のとき\(f(x)<0\)です。
ここまでで,以下の領域に\(~f(x)~\)が存在することが分かります。斜線部は「存在しない領域」です。
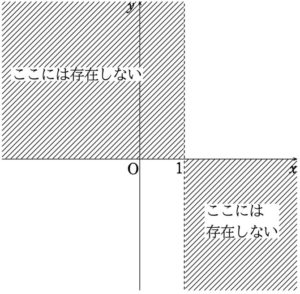
極限を,大まかに調べる
次は極限です。\(x \to +\infty\)のとき,\(e^x~\)と\(~x-1~\)はどちらも\(+\infty\)となりますが,その速さは\(~e^x~\)の方が圧倒的に早いので,結果として\(~f(x)~\)は\(+\infty\)となります。
また,\(x \to -\infty\)のとき,\(~e^x~\)は0に近づき,\(\dfrac{1}{x-1}~\)も0に近づきます。結果として,\(~f(x)~\)は負の値をとりながら\(~0~\)に近づきます。
この時点で,グラフはこんな感じです。
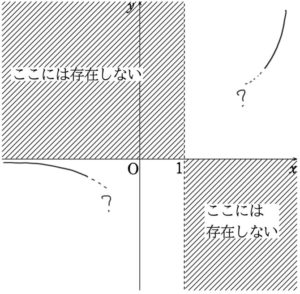
あとは\(~x=1~\)の周辺を調べます。
\(~x \to 1+0~\)のとき,\(e^x~\)は\(~e~\)に近づき,\(\dfrac{1}{x-1}~\)は\(+\infty\)となります。結果として\(~f(x)~\)は\(+\infty\)となります。
また,\(~x \to 1-0~\)のとき,\(e^x~\)は\(~e~\)に近づき,\(\dfrac{1}{x-1}~\)は\(-\infty\)にとなります。結果として\(~f(x)~\)は\(-\infty\)となります。
ということで,\(y=f(x)~\)のグラフの概形が以下のように分かりました。
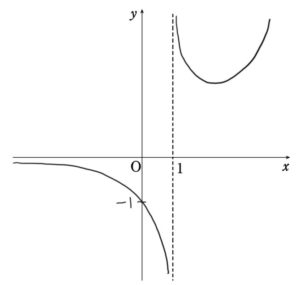

手書きで申し訳ありません(笑)。
もちろん,この方法では分からないこととして,極小値を取る点はどのあたりにあるのか,他に極値を取る点はないのか,などがあります。でも,極値が分からなくても解ける問題はありますし,概形が分かるだけでもかなりの情報となります。使える場面はあると思いますので,ぜひマスターしておきましょう。
早速やってみたい人は,次の関数のグラフを考えてみましょう!
- \(y=\dfrac{\log x}{x}\)
- \(y=\dfrac{x^2}{e^x}\)
- \(y=\dfrac{x}{(x+1)(x-2)}\)
まとめ
いかがでしたか?
グラフを描くのに,何でもかんでも微分する必要はないということですね。

ただし,「グラフの概形をかけ」や「極値を求めよ」などの問題は必ず微分しなければなりません。そこは手を抜かないように(笑)。
微分しなくてもおおよそのグラフの形が分かれば,問題が解きやすくなることがあります。手抜きできるところは大いに手抜きしましょう(笑)。


