絶対値のある方程式・不等式について，
「絶対値の定義は知ってるけど，イマイチわかりにくいし，解けないんだよなあ・・・」
と思っている人はいませんか？
そんなあなたは，絶対値を含んだ方程式・不等式の解き方を，整理できていないのかもしれません。
この記事を読んで解き方を整理し，すらすらと解けるようになりましょう。
- 絶対値があるとビビってしまう高校生・受験生
- 絶対値の場合分けがこんがらがってしまう人
まずは3つの解法を確認しておこう
まず解法が3つあることを確認しておきましょう。
3つともわかりますか？
【解法1】場合分けを用いる（これが大原則）
絶対値記号は，記号の中の数が正か負かで，次のように場合分けできます。
これを利用して，正の場合と負の場合に分けて計算します。
【解法2】まるごと絶対値型の解法を利用する
「まるごと絶対値型？何じゃそりゃ？」
聞いたことがなくても，無理はありません。私が命名した言葉だからです(笑)。
左辺が絶対値記号で覆われていて，右辺が正の定数であるときに使える解法です。
以下にまとめておきましょう。
\(~a~\)は正の定数とする。
\begin{align*} |x|=a \quad & \Longleftrightarrow \quad x= ± a \\ |x| < a \quad & \Longleftrightarrow -a < x < a \\ |x| > a \quad & \Longleftrightarrow x < -a,~ a < x \\ \end{align*}「ああ，これね」という声が聞こえてきそうです(笑)。学校でそれなりに勉強した人であれば知っているはずです。
でも，いつでも使えるわけじゃないっスよね？特殊な形だし
そうですね。確かにその通りです。でも，みんなが思っているよりも，使う場面は多いかもしれません。後で問題を使って説明します。
【解法3】グラフを利用する
3つめの解法は「グラフを利用する」です。
「場合分け」と「まるごと絶対値型」は知っていても，「グラフ」を利用することを意識している人は，意外に少ないと思います。
この,「グラフを利用する」解法を使えるか使えないかで，入試の実戦力はかなり変わってきます。ぜひマスターしましょう。
基本問題を解いて学ぼう
では，3つの解法について，問題を解きながら学んでいきましょう。まず，次の基本問題を解いていきます。
次の不等式を解け
\( (1) \quad |x-3|>2 \qquad (2) \quad |x+1|+|x-2| \leqq 4-x \)
場合分けするときの大切な手順
(1)を場合分けして解いてみます。
ただ，やや問題がある解答にしておきます。どこに問題があるか，考えてみて下さい。
(1)（誤答？）
\( [1] x \geqq 3 \)のとき \(\quad |x-3|>2~\)より
\begin{align*} x-3 \geqq 2 \\ \therefore x>5 \end{align*}\( [2] x < 3 \)のとき \(\quad |x-3|>2~\)より
\begin{align*} -(x-3) \geqq 2 \\ \therefore x<1 \end{align*}[1][2]より，\( x < 1,~ 5 < x \)
答えは間違っているわけではありません。しかし，あまりよくない解答だなあ，と思っています。実際，この答案を見たら注意することにしています。どこが問題なのか分かりますか？
それは，「場合分けしたときの条件を確認していないこと」です。
これは場合分け全般について言えることなのですが，場合分けして一応の答えが出たところで，「場合分けしたときの条件を満たすかどうか確認する」という大切な手順があります。
これはとても重要です。
場合分けしたということは，ある条件の下で式を解いていることになります。
ということは，出てきた解答が，元の条件を満たしているかどうか，確認しなければならないのです。場合分けした条件を満たしていなければ，それは解とは認められないのです。
確認をすると，次のような解答になります。
(1)（正しい解答）
\( [1] x \geqq 3 \)のとき \(\quad |x-3|>2~\)より
\begin{align*} x-3 > & 2 \\ \therefore x > & 5 \qquad \text{これは，}x \geqq 3 \text{を満たす。} \end{align*}\( [2] x < 3 \)のとき \(\quad |x-3|>2~\)より
\begin{align*} -(x-3) > & 2 \\ \therefore x< & 1 \qquad \text{これは，}x < 3 \text{を満たす。} \end{align*}[1][2]より，\( x < 1,~ 5 < x \)
ほとんど変わりませんが，[1][2]ともに，場合分けしたときの条件を満たしているかどうかを確認していますね。こういうところをおろそかにしていると，本番でうっかり，解でないものを解としたりすることになります。場合分けの正しい手順を身につけておきましょう。
場合分けって，めんどくさいっスねえ。できればやりたくないっス・・・
だよね。実はこの問題，普通は場合分けしないで解きます。左辺がまるごと絶対値記号になってますからね。通常は次のように解きます。
まるごと絶対値型の方が簡単
\( |x-3|>2~\)より \begin{align*} x-3 < -2,~ 2 < x-3 \\ \therefore x<1,~ 5<x \end{align*}
場合分けすることに比べると，とてもシンプルに解くことができますね。
絶対値記号については，場合分けして解くことが大原則です。しかし，いつもいつも場合分けしていては，問題を解くのに時間がかかりすぎたり，ミスが多くなったりします。
まるごと絶対値型の場合は，迷わずこのように解きましょう。
絶対値記号が増えても場合分けなら解ける
次は(2)を場合分けして解きます。
\( (2) \quad |x+1|+|x-2| \leqq 4-x~ \)について
\([1]~x < -1 ~\)のとき
\begin{align*} -(x+1)-(x-2) &\leqq 4-x \\ -2x+1 &\leqq 4-x \\ x &\geqq -3 \\ \text{条件}~x<-1 \text{より} \qquad -3 \leqq x & < -1 \end{align*}\([2]~ -1 \leqq x < 2~ \) のとき
\begin{align*} (x+1)-(x-2) & \leqq 4-x \\ 3 & \leqq 4-x \\ x & \leqq 1 \\ \text{条件} -1 \leqq x < 2 ~ text{より} \qquad -1 \leqq x & \leqq 1 \end{align*}\([3]~2 \leqq x ~\)のとき
\begin{align*} (x+1)+(x-2) & \leqq 4-x \\ 2x-1 & \leqq 4-x \\ x & \leqq \frac{5}{3} \\ \text{これは，条件}~2 \leqq x ~\text{を満たさないので不適} \end{align*}[1][2][3]より
\begin{align*} -3 \leqq x \leqq 1 \end{align*}[1][2][3]それぞれ，場合分けしたときの条件を確認していることに注意して下さい。
なお，この(2)は，まるごと絶対値型の解法は使えません。左辺を見れば判断できますよね。
グラフを利用する解法まで身につけておこう
【解法1】場合分け，【解法2】まるごと絶対値型，の2つの解法を見てきました。この2つについてマスターしている人は多いと思います。しかし，実戦的にはもう一つの解法，【解法3】グラフの利用，をマスターしておきたいところです。
今解いたばかりの基本問題2問について，グラフを用いたらどうなるか，見てみましょう。
(1)
\begin{align*} |x-3|>2 \end{align*}\( y=|x-3|~\)と\(y=2~\)のグラフを用いて考える。
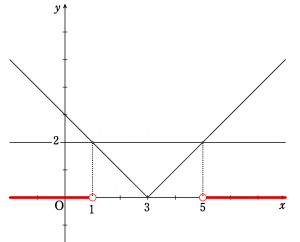
上のグラフより
\begin{align*} x < 1,~ 5 < x \end{align*}(2)
\begin{align*} |x+1|+|x-2| \leqq 4-x \end{align*}\( y=|x+1|+|x-2|~\)と\(y=4-x~\)のグラフを用いて考える。
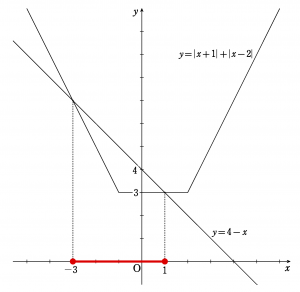
上のグラフより
\begin{align*} -3 \leqq x \leqq 1 \end{align*}どうですか？
とてもシンプルに解くことができますよね。
もちろん，グラフが書けなければなりませんが，(1)(2)あたりは慣れれば簡単に書くことができます。
ぜひグラフを利用した解法までマスターしておきましょう
実戦問題を解いてみよう
ではこれまで学んだことを使って，実戦問題を解いてみましょう。あなたなら，どの解法で解きますか？
不等式\(~||x-2|-5| < 3 ~\)を解け。
なんかめんどくさそうな問題っスねえ・・・
でも，左辺をよく見てごらん。入れ子になっているからわかりにくいけど・・・
あ！まるごと絶対値型っスね！
（2）\(\quad\) 不等式\(~||x-2|-5| < 3 ~\)より
\begin{align*} -3 < |x-2|-5 & < 3 \\ 2 < |x-2| & < 8 \end{align*}左側の不等式，\(|x-2|>2~\)より
\begin{align*} x-2 < -2,~ 2 < x-2 \\ x < 0,~ 4 < x \cdots [1] \end{align*}右側の不等式，\(|x-2| < 8~\) より
\begin{align*} -8 < x-2 < 8 \\ -6 < x < 10 \cdots [2] \end{align*}[1]かつ[2]より，\(-6 < x < 0,~ 4 < x < 10\)
おお！意外といけるっスね！まるごと絶対値型，恐るべし！
いや，恐れなくてもいいんだけど(笑)。
まるごと絶対値型を使う場合，外側の絶対値から外していることに注目しておこう。
ちなみに，場合分けで解くときは，内側から外した方がやりやすいと思うよ。時間が合ったらやってみよう！めんどくさいけどね。
（2）\(\quad\) \(~||x-2|-5| < 3 ~\)
まず\( y=||x-2|-5|~\)のグラフを描くことを考える。
\(y=|x-2|\)のグラフを，\(~y~\)軸方向に\(~-5~\)平行移動し，\(y=|x-2|-5~\)のグラフをつくる。
次に，\(y=|x-2|-5~\)のグラフの\(~x~\) 軸より下の部分を上に折り返す。できたグラフは\(~y=||x-2|-5|~\)のグラフである。
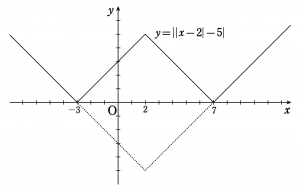
この\(~y=||x-2|-5|~\)のグラフと\(y=3~\)のグラフを用いて考える。
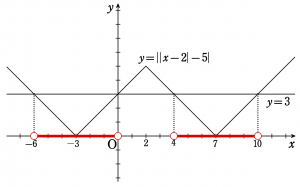上のグラフより \begin{align*} -6 < x < 0,~ 4 < x < 10 \end{align*}
どうですか？
グラフも平行移動と折り返しだけで描くことができるので，あっさり解けるでしょう？
グラフを用いた解法は，問題の見通しがかなり良くなるので，ぜひマスターしておきましょう！
まとめ
絶対値記号を扱うに当たって，場合分けはできなければなりません。
しかしそれだけでは不十分です。
まるごと絶対値型を見抜いて解く方法，そしてグラフを用いて解く方法もマスターしましょう。
それが，入試における実戦力となります。
- 絶対値は原則場合分けで解く
- まるごと絶対値型は簡単に解ける
- グラフを用いて解くのも有効です
この記事が，頑張っているあなたのお役に立てることを願っています。
