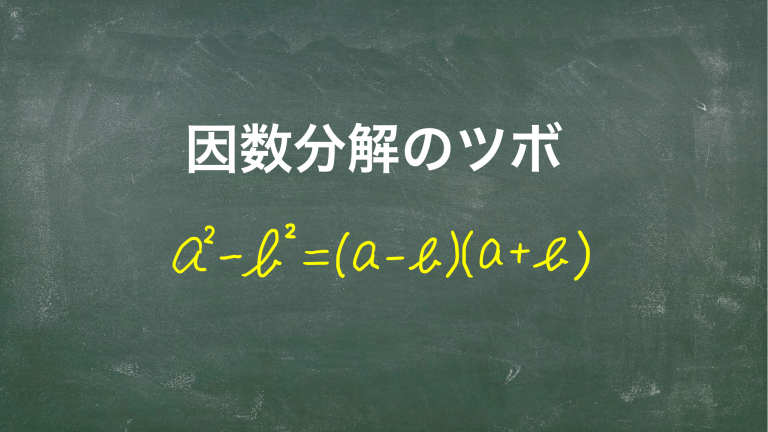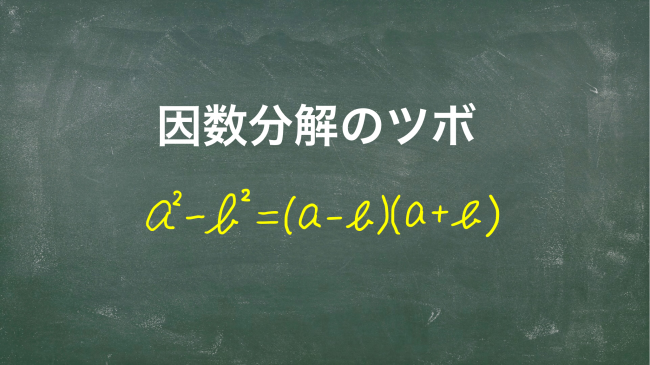【数Ⅰ】勘に頼らずにできる！因数分解のツボ（２）

前回に続き，因数分解のツボについての記事です。勘に頼っていると，解けるときと解けないときがあるはずです。必ず解けるようになるために，正しい手順を身につけましょう。

前回の記事はこちらです。

勘に頼らずにできる！因数分解のツボ（１）

〔２〕最も重要！次数の低い文字について整理する
1. 解法にも重要性の違いはある
2. 「次数の低い文字について整理する」は重要なポイント
例題でわかる重要性
この記事のまとめ

〔２〕最も重要！次数の低い文字について整理する

解法にも重要性の違いはある

因数分解をマスターするうえで，最も大切な部分を紹介しよう。ヒット曲には盛り上がるサビの部分があるように，フランス料理にはメインディッシュがあるように，因数分解にも最も重要な手法というものがあるのだ！

・・・たとえがイマイチ微妙っす・・・。早く教えてくださいよ。

「次数の低い文字について整理する」は重要なポイント

（・・・ちょっと恥ずかしい）コホン，因数分解で重要なこと，それは「次数の低い文字で整理する」という手法だ。学校の先生からも習っただろう？

うーん，聞いたことあるような気もするけど・・・因数分解だけでたくさん習ったので，そのうちの1つにあったような気がするっス。

そこだよ，そこが問題なんだ。教科書に練習問題がいろいろ載っているよね。それらをなんとなく解いているだけでは，重要なポイントに気付かないんだ。たくさんある因数分解の手法の中でも，最も重要な手法がこの「次数の低い文字について整理する」という手法なんだ。

学校の先生は，そこまでは強調していないっス。授業では淡々と問題を解いていくだけでした。

たぶん，問題を解かせて解説することに必死なんだろうね。ただ，解き方をいろいろ紹介するだけではまだ不十分だ。解き方には重要度に違いがあるからね。思い出してほしい。因数分解を勘に頼らずに解こう，というのがこの記事のテーマだったよね。そのための重要なポイントがここだ。因数分解のツボはここだ，と言ってもいいだろう。

へえ。わかりました。「次数の低い文字について整理する」ですね，しっかり覚えておきます！

例題でわかる重要性

では具体的に見ていこう。次の問題を利用して説明しよう。どう？解けそうかな？

因数分解しなさい。

\( x^2-(a+b)x+ab \)
\( x^2+xy-2y^2+2x+7y-3 \)
\( a^3(b-c)+b^3(c-a)+c^3(a-b) \)

ん？(1)は公式じゃないですか。\( x^2+(a+b)x+ab=(x+a)(x+b) \)ですよね？

もちろんそうだ。でもここはあえて公式を使わないで解いて欲しい。

えーと「次数の低い文字について整理する」でしたね・・・おー本当だ，ちゃんと解けたっス！

だろう？では全部見てみよう。

(1) \begin{align*} x^2-(a+b)x+ab=& (x^2-bx)-(x-b)a \\ =& (x-b)x-(x-b)a \\ =& (x-a)(x-b) \end{align*} (2) [ \begin{align*} x^2+xy-2y^2+2x+7y-3=& x^2+(y+2)x-(2y^2-7y+3) \\ =& x^2+(y+2)x-(2y-1)(y-3) \\ =& \left\{ x+(2y-1) \right\} \left\{ x-(y-3) \right\} \\ =& (x+2y-1)(x-y+3) \end{align*} ] (3) \begin{align*} a^3(b-c)+b^3(c-a)+c^3(a-b)=& (b-c)a^3-(b^3-c^3)a+bc(b^2-c^2) \\ =& (b-c)\left\{ a^3-(b^2+bc+c^2)a +bc(b+c) \right\} \\ =& (b-c)\left\{ (c-a)b^2 +c(c-a)b -a(c^2-a^2) \right\} \\ =& (b-c)(c-a)\left\{ b^2+bc-a(c+a) \right\} \\ =& (b-c)(c-a)\left\{ (b-a)c +(b^2-a^2) \right\} \\ =& (b-c)(c-a)(b-a)\left\{ c+(b+a) \right\} \\ =& -(a-b)(b-c)(c-a)(a+b+c) \end{align*}

ううう・・・(2)は何とか基本公式のたすき掛けだと気づきましたけど，(3)は難しいっス・・・

(3)については解説を加えよう。1行目で\(~a~\)について整理しています。そのときの\(~a~\)の係数\(~b^3-c^3,~\)定数項\(~b^2-c^2~\)はそれぞれ\( (b-c)(b^2+bc+c^2),~(b-c)(b+c) \)と因数分解できます。ですから2行目で\( (b-c) \)で括っています。

ふむふむ。

\( (b-c) \)で括った残りの右かっこの中を見ると，次数が低いのは\(~b,~c~\)です。ですから，3行目で右かっこを\(~b~\)について整理しています。すると，また\(~c-a~\)で括ることができることが分かりますので，4行目で\( (c-a) \)で括っています。

おお！また次数の低い文字について整理するのか！

まだまだ。そのあと残った右かっこを見ると，次数が低いのは\(~c~\)ですから，5行目で\(c~\)について整理します。すると，\(b-a~\)で括れることがわかるので，6行目で\((b-a)~\)で括ります。

おお！また使うのか！結局3回使うんですね？すげー！

そう，基本公式を当てはめても分からない場合は，この「次数が低い文字について整理する」という手法を使えば，かなり見えやすくなるはずだ。「困った時の神頼み」ということわざがあるが，「困ったときには整理する」も新しいことわざとして覚えておいてくれ！

・・・（笑ってほしいのかもしれないが，スルーしておこう）・・・ちなみに最後の7行目はいるんですか？

ここは，数学的には6行目と変わらないのだが，慣例としてこう変形するようになっている。\(a \to b \to c \to a \)と循環するよう整理するんだ。そうした方が美しいだろう？

わかるようなわからないような・・・数学ができる人って，それまでずっと理論的に話していたのに，いきなり「美しい」なんて情緒的な言葉を使うんだよなあ・・・それって矛盾してるように見えるんスけど・・・

えっ？何か言った？

いえ，何でもないっス。（まだ3番目の話を聞いていないので，機嫌を損ねないようにしとこう。）

次の記事，「勘に頼らずにできる！因数分解のツボ(3)」に続く。